Batch 2 - Class 298 - Pascal's Triangle

Zoom: send meeting Id and password

Start recording

Preclass Exercise:

Design your own game on lines of Hopper. Analyze the fairness of the game.

Attendance: Raghav, Anika, Aneesh, Tarush, Kabir, Yatharth, Rhea Chadha, Ryan Chadha, Advay, Vivaan, Adyant, Ayush, Nikhil, Aarav, Aneesh, Aarushi, Ekagra, Mihir

Class Notes: (repeat from class 221 - Shikhar, Vansh, Aarkin, Advay, Kabir were present)

Let's play an arcade game. https://www.youtube.com/watch?v=nOenO-JLD5w - you have a grid of obstructions and marbles fall through those. At each point, the marble can take the left or the right fork, and fall till the end. At the end we have a capture. We finally look at which slot the marbles fall into.

Let students toss coins and run a few iterations
Run an excel simulation (Pascals triangle game excel file) to illustrate results at scale
Why is this happening? Can we provide an analytical explanation rather than a simulation based one?

Consider choice at each step - the marble could go either to the left or right with equal probability. What are the (analytical) chances of the marble landing in any given slot?

How does this correlate to the number of paths the marble can take in getting to a particular slot?
Are all paths equally likely?
Can you now derive the chances of getting to a particular slot?

The choice at each step can also be represented as a string of L and R (or 0 and 1). Consider a particular slot - in any string representing the marble falling into that slot, how many 0s and 1s must occur?

Hence the number of ways the marble can land up in a particular mth slot must also equal the number of ways of choosing "m" 1s in a string of 0s and 1s of length n.
Since the assignment of 0s and 1s to L and R is arbitrary, we can also swap them, and we could have also chosen "m" 0s. Hence the symmetry in the pattern.

Look at the binomial expansion of (n+m)^k - work out for (n+m)^4 - why are these coefficients same as numbers in pascals triangle?
Lets now draw a full pascal's triangle and examine its properties (explain the properties both in terms of the marbles falling, and their combinatorics rationale)

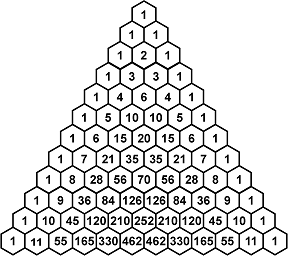
Show that any number is equal to sum of numbers on previous right diagonal, or previous left diagonal. Why does this exist? Can we think of this in terms of ways of choosing m objects from n objects?
There seen to be powers of 11 on each row. Why?

Aarushi's poser

I was attempting a problem which required me to know the relation between the number of divisors of a number and its prime factors.

Here I know that 30 is 2*3*5 so I constructed a flowchart taking HCF of the numbers at every level to find the divisors.

I noticed a Pascal's triangle layer here - the number of divisors of the layers goes 1 3 3 1.

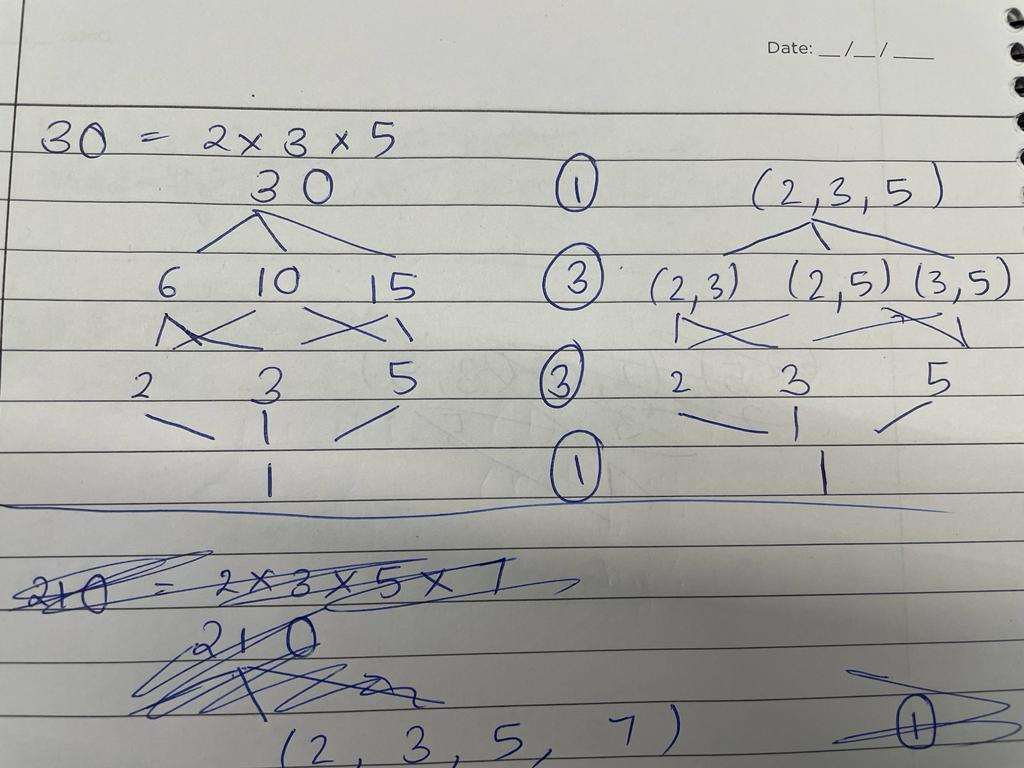
I tried it with 210 and I got the next layer - 1 4 6 4 1

I was only testing with the powers of all prime numbers equal to 1.

I tried with 60 so that I could have 2 * 2.

This is when things got really interesting.

Naturally, some factors repeated on every row . (I have circled them)

The number of extra factors also have a pattern that is from the Pascal's triangle - 1 2 1.

The total number of divisors becomes (1 4 6 4 1) - (1 2 1)

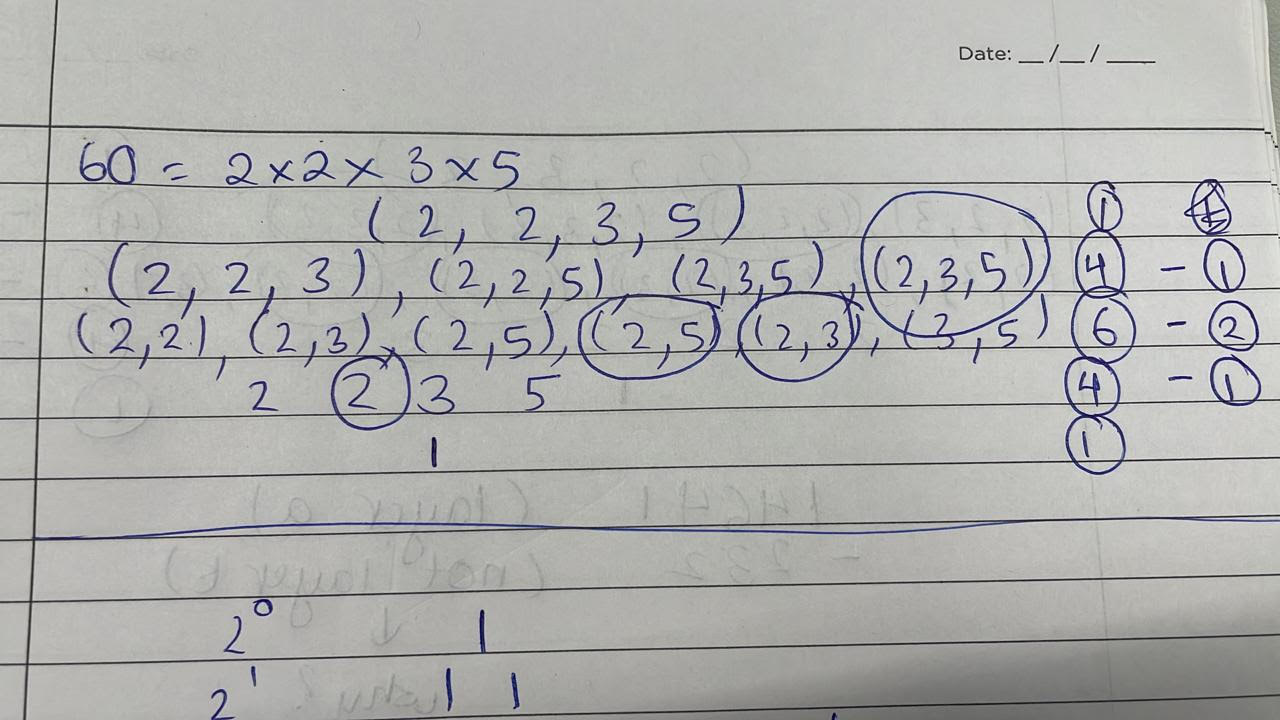
In other cases as well the pattern of the repeat divisors was two rows behind the normal pattern.

If I increased 2 to the power of 3, then the same formula applies, except we now subtract 2 4 2 or 2 times the previous one (1 2 1)

Strangely, the Pascal's triangle pattern is not visible to me if I increase the power of both 2 and 3 to 2 (2*2*3*3)

Can you tell me why it doesn't work here? And why were we seeing this pattern in the first place?

Homework

References:

https://www.mathsisfun.com/pascals-triangle.html

http://www.cut-the-knot.org/arithmetic/combinatorics/PascalTriangleProperties.shtml